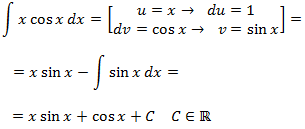Aprendizajes esperados.
Tratamiento analítico de las integrales definidas e indefinidas y uso intuitivo de los procesos infinitos y las situaciones límite.
Ejercicios sobre integral definida.
liks de paginas de apoyo:
1.- 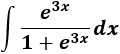
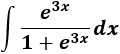
Atendiendo a la tabla, escogemos el cambio de variable
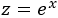
Despejamos aplicando logaritmos:
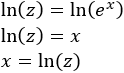
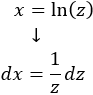
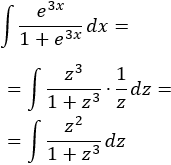
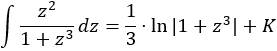
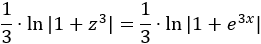
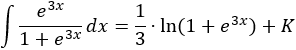
-----------------------------------------------------------------------------------------------
2.- 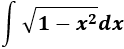
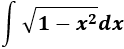
Teniendo en cuenta la tabla, escogemos el cambio
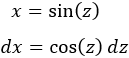
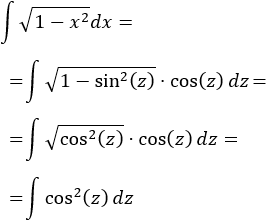
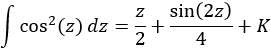
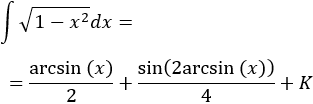
-----------------------------------------------------------------------------------------------
3.-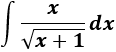
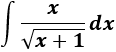
Escogemos el cambio de variable
radicando para que desaparezca la raíz cuadrada:
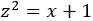 Despejamos y derivamos:
Despejamos y derivamos:
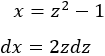 Sustituimos en la integral y simplificamos:
Sustituimos en la integral y simplificamos:
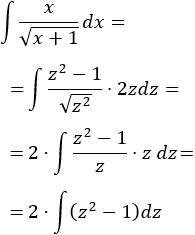 Calculamos la integral:
Calculamos la integral:
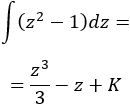 Deshacemos el cambio de variable:
Deshacemos el cambio de variable:
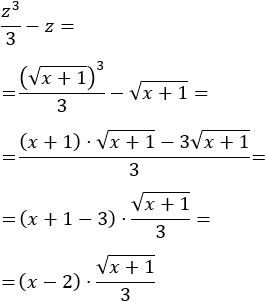 Por tanto,
Por tanto,
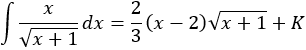
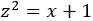
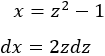
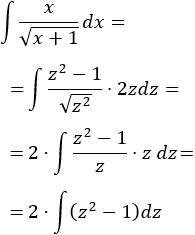
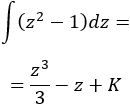
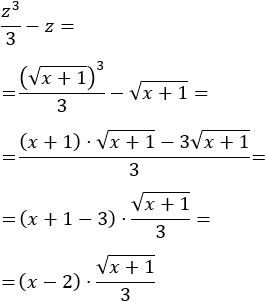
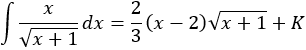
-----------------------------------------------------------------------------------------------
4.- 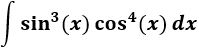
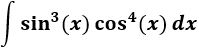
Como el exponente del seno es impar, utilizaremos el cambio
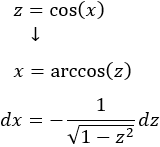
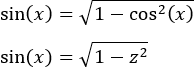
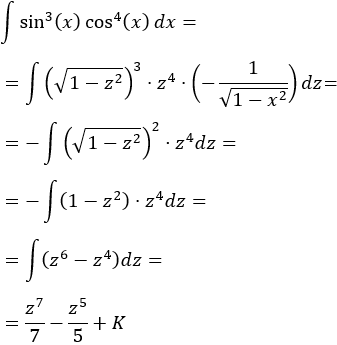
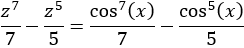
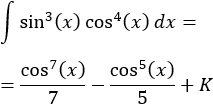
Ejercicios sobre Integracion por Partes.
1.-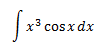
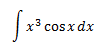
Aplicaremos integración por partes 3 veces para reducir el exponente del monomio:
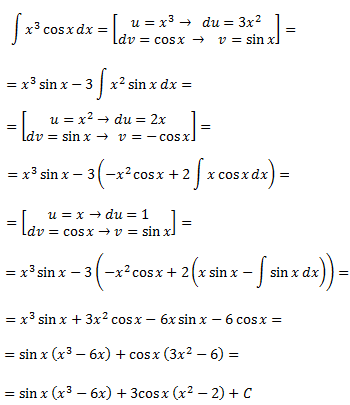
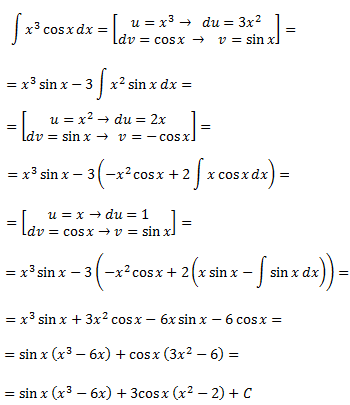
-----------------------------------------------------------------------------------------------
2.-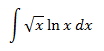
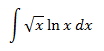
Si escogemos dv = ln(x), no podremos obtener fácilmente v. Es mejor escoger
u = ln(x)
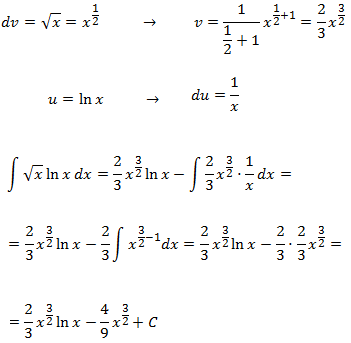
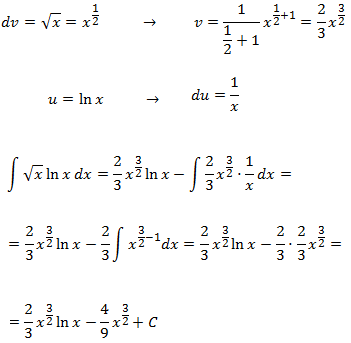
-----------------------------------------------------------------------------------------------
3.-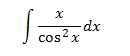
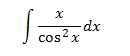
Escogemos u = x para reducir su exponente (y por tanto, desaparece x).
Notemos que la primitiva de
es inmediata.
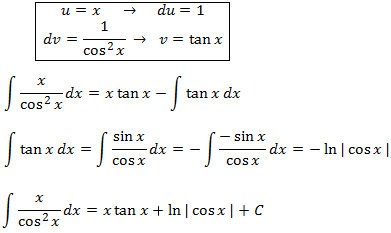
Notemos que la primitiva de
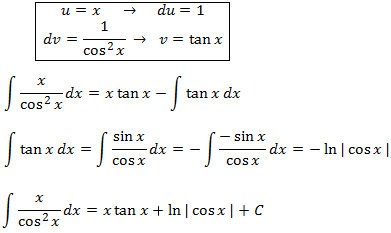
-----------------------------------------------------------------------------------------------
4.-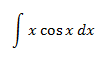
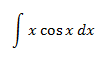
Integramos por partes:
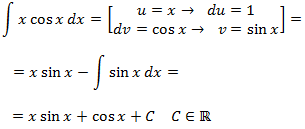 Nota: al igual que en el ejercicio anterior, como no importa si cos x es
u ó dv (ya que obtenemos un sinus), elegimos u = x para disminuir su grado (y así
desaparece la x). Si escogemos dv = x, aumentamos su grado:
Nota: al igual que en el ejercicio anterior, como no importa si cos x es
u ó dv (ya que obtenemos un sinus), elegimos u = x para disminuir su grado (y así
desaparece la x). Si escogemos dv = x, aumentamos su grado: