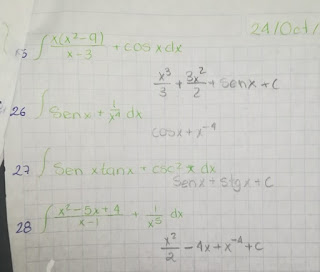Aprendizajes esperados.
Anti-derivadas de las funciones elementales (Algebraicas y Trascendentales).
Constante
El ejemplo de la derivada 𝑓´(𝑥) = 6𝑥 + 5, seguro propusieron 𝑓(𝑥) = 3𝑥2 +
5𝑥 pero ¿es la única función que al derívala obtenemos 𝑓´(𝑥) = 6𝑥 + 5?
La respuesta es no, porque por ejemplo la función 𝑓(𝑥) = 3𝑥2 + 5𝑥 + 1 también cumple
que al derivarla obtenemos la función 𝑓´(𝑥) = 6𝑥 + 5.
Cuando no imponemos la condición de que pase por un punto, nos
quedamos con una familia de funciones, debido a que la constante
ocasiona una traslación vertical a la gráfica de la ant-derivada y = f(x).
Cuando impongamos una condición que deba satisfacer la anti-derivada de la función dada, por ejemplo, que pase por un punto dado, tendremos la posibilidad de reducir toda una familia de funciones a una sola función.
Regresemos a la función 𝒇(𝒙) = 𝟔𝒙 + 𝟓 y calculemos la antiderivada que pase por el
punto (0,1).
Primero calculamos la antiderivada y después nos preocuparemos por que pase por el
punto dado. • La antiderivada de la función es: 𝑓(𝑥) = 3𝑥2 + 5𝑥 + 𝐶 • Si la antiderivada debe pasar por el punto A(0,1), entonces ésta debe satisfacer las coordenadas de ese punto. • Matemáticamente, tenemos:𝑓(0) = 1. • Por lo tanto 𝑓(0) = 3(02) + 5(0) + 𝐶 = 1 ⟹ 𝐶 = 1
Entonces, la constante de integración es C = 1, y la antiderivada particular que satisface la condición de pasar por el punto (0,1) es: 𝑓(𝑥) = 3𝑥2 + 5𝑥 + 1
Ahora el resultado no fue una familia de funciones, dado que debían satisfacer la condición de pasar por el punto dado.
Ejercicios sobre integral indefinida.
Integral Definida como área.
Teorema fundamental del cálculo:
f(X) es la razón de cambio de y=f(x) con respecto a x. f(b)-f(a) es el cambio en y cuando x cambia de a hacia b.
Aplicaciones del Cálculo Integral a Física.
Si un objeto se mueve a lo largo de una línea recta con función de posición 𝑠(𝑡), entonces su velocidad es 𝑣(𝑡) = 𝑠´(𝑡), de modo que:
∫ 𝑣(𝑡)𝑑𝑡 = 𝑠(𝑡2) − 𝑠(𝑡1) 𝑡2 𝑡1
es el cambio de la posición o desplazamiento de la partícula durante el periodo desde 𝑡1 hasta 𝑡2. Si quiere calcular la distancia recorrida durante el intervalo, tiene que considerar los intervalos cuando 𝑣(𝑡) ≥ 0 (la partícula se mueve hacia la derecha) y también los intervalos cuando 𝑣(𝑡) ≤ 0 (la partícula se mueve hacia la izquierda). En ambos casos la distancia se calcula al integrar |𝑣(𝑡)|, la magnitud de la rapidez. Por consiguiente:
∫ | 𝑣(𝑡) | 𝑑𝑡 = 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑡𝑜𝑡𝑎𝑙 𝑟𝑒𝑐𝑜𝑟𝑟𝑖𝑑𝑎 𝑡2 𝑡1
En la siguiente figura se muestra cómo interpretar el desplazamiento y la distancia recorrida en términos de las áreas debajo de una curva de velocidad.
𝑑𝑒𝑠𝑝𝑙𝑎𝑧𝑎𝑚𝑖𝑒𝑛𝑡𝑜 = ∫ 𝑣(𝑡)𝑑𝑡 = 𝐴1 − 𝐴2 + 𝐴3 𝑡2 𝑡1
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 = ∫ |𝑣(𝑡)|𝑑𝑡 = 𝐴1 + 𝐴2 + 𝐴3 𝑡2 𝑡1
La aceleración del objeto es 𝑎(𝑡) = 𝑣´(𝑡), por eso
∫ 𝑎(𝑡)𝑑𝑡 = 𝑣(𝑡2) − 𝑣(𝑡1) 𝑡2 𝑡1
es el cambio en la velocidad, desde el instante 𝑡1 hasta 𝑡2.
Solución:
a. Usando la información tenemos que ∫ 𝑣(𝑡)𝑑𝑡 = 𝑠(𝑡2) − 𝑠(𝑡1) 𝑡2 𝑡1 , entonces el desplazamiento es:
𝑠(𝑡2) − 𝑠(𝑡1) = ∫ 𝑣(𝑡)𝑑𝑡 𝑡2 𝑡1
𝑠(4) − 𝑠(1) = ∫ 𝑣(𝑡)𝑑𝑡 4/1
𝑠(4) − 𝑠(1) = ∫ (𝑡2 − 𝑡 − 6)𝑑𝑡 4/1
𝑠(4) − 𝑠(1) = [𝑡3/3 − 𝑡2/2 − 6𝑡] 1/4
𝑠(4) − 𝑠(1) = −9/2
Esto significa que la partícula se desplaza 4.5 metros hacia la izquierda. b. Si quiere calcular la distancia recorrida durante el intervalo, tiene que considerar los intervalos cuando 𝑣(𝑡) ≥ 0 (la partícula se mueve hacia la derecha) y también los intervalos cuando 𝑣(𝑡) ≤ 0 (la partícula se mueve hacia la izquierda). Entonces para conocer los signos de la velocidad usemos su gráfica para determinar en qué intervalos son positivos y negativos 𝑣(𝑡).
Análisis de la gráfica en el intervalo [1,4]: • En el intervalo de [1,3], la gráfica v(t) es negativa • En el intervalo de [3,4], la gráfica v(t) es positiva
Entonces la distancia se divide en dos integrales ya que una es negativa y otra es positiva.
Ejercicios sobre integral definida.
1. Un objeto se mueve con movimiento rectilíneo de modo tal que su velocidad en el instante t es 𝑣(𝑡) = 𝑡2 − 2𝑡 metros por segundo. Calcular: a. El desplazamiento del objeto durante los tres primeros segundos. b. La distancia recorrida durante ese tiempo. Considera la gráfica de la velocidad 𝑣(𝑡) = 𝑡2 − 2𝑡
2. Un objeto se mueve en línea recta y su velocidad v en el tiempo t está dada por 𝑣(𝑡) = 1/5 (𝑡3 + 𝑡2 + 𝑡). Donde t está medido en segundos y v(t) está medida en metros/segundo. Considera la gráfica de velocidad Calcular: a. La distancia que recorre a los primeros 3 segundos.
